Perhitungan Weighted Product Model Untuk Sistem Pendukung Keputusan
4/21/2018 • Algorithm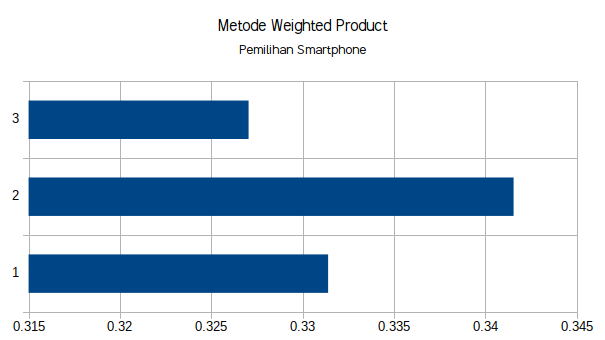
Weighted Product (WP) adalah himpunan berhingga dari alternatif keputusan yang dijelaskan dalam beberapa hal kriteria keputusan. Metode ini merupakan salah satu metode penyelesaian yang ditawarkan untuk menyelesaikan masalah Multi Attribute Decision Making (MADM).
Contoh kasus ketika menentukan smartphone yang sesuai dengan kebutuhan kita. Pada contoh ini ada tiga smartphone yang akan menjadi alternatif pilihan:
A1 = Samsung Galaxy J5
A2 = Xiaomi Redmi 4X
A3 = Oppo A57Ada empat kriteria yang menjadi acuan dalam pemilihan smartphone, yaitu:
C1 = Harga
C2 = Kapasitas RAM/ROM
C3 = Kualitas Kamera
C4 = Kapasitas BateraiPembobotan setiap kriteria dihitung berdasarkan tingkat kepentingannya. Pada kasus ini terdapat lima tingkat kepentingan:
Sangat Tidak Penting = 1
Tidak Penting = 2
Cukup Penting = 3
Penting = 4
Sangat Penting = 5Tentukan kategori Cost dan Benefit dari setiap kriteria tersebut. Cost merupakan biaya, semakin besar nilainya akan semakin buruk. Benefit merupakan keuntungan.
Cost = Harga
Benefit = Kapasitas RAM/ROM, Kualitas Kamera, Kapasitas Baterai.Tentukan nilai bobot preferensi dari masing-masing kriteria:
C1 = Cukup Penting(3)
C2 = Sangat Penting(5)
C3 = Cukup Penting(3)
C4 = Penting(4)Dan nilai kriteria (C) dari setiap alternatif (A) kita berikan berdasarkan spesifikasi smartphone sesuai dengan kriteria yang telah kita tentukan sebelumnya.
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| A1 | 82 | 76 | 85 | 76 |
| A2 | 75 | 80 | 75 | 82 |
| A3 | 80 | 76 | 79 | 75 |
Nilai bobot preferensi jika kita buat larik akan seperti ini w=4 Kemudian kita lakukan perbaikan bobot dengan formula berikut:

| Keterangan: | |
|---|---|
| W | Bobot preferensi |
| Wj | Bobot preferensi pada indeks j |
| ∑Wj | Jumlah seluruh bobot |
Kita tentukan nilai ∑Wj,
∑Wj = 3 + 5 + 3 + 4 = 15
lalu kita hitung masing-masing bobot kriteria,
W1 = 3 / 15 = 0.2
W2 = 5 / 15 = 0.33
W3 = 3 / 15 = 0.2
W4 = 4 / 15 = 0.27
Selanjutnya kita tentukan nilai vektor S dengan formula berikut:

Maka,
S1 = (82-0.2) (760.33) (850.2) (760.33) = 13.539
S2 = (75-0.2) (800.33) (750.2) (820.33) = 13.954
S3 = (80-0.2) (760.33) (790.2) (750.33) = 13.362
Kriteria yang merupakan kategori Cost akan berpangkat bobot perbaikan yang bernilai minus.
Lalu kita tentukan nilai vector yang akan digunakan untuk menghitung preferensi (Vi) sebagai perengkingan. Formulanya seperti berikut:

atau sederhananya seperti ini:

Tentukan nilai ∑Sj agar mempermudah perhitungan,
∑Sj = 13.54 + 13.95 + 13.36 = 40.856
V1 = 13.54 / 40.856 = 0.331
V2 = 13.95 / 40.856 = 0.342
V3 = 13.36 / 40.856 = 0.327
Maka dapat kita simpulkan nilai tertinggi adalah V2 atau (A2) Xiaomi Redmi 4X merupakan pilihan alternatif terbaik sesuai pembobotan yang diberikan oleh pengambil keputusan.
Di tulisan berikutnya kita akan mengimplementasikan perhitungan metode Weighted Product ini kedalam bahasa pemrograman Java. Lihat Implementasi Weighted Product Model menggunakan Java.